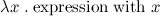As a beginner Haskell programmer I still remember its horrors. Time to write them down. It is my first functional language, so I have to learn new concepts and new language in parallel, but it is fun. I hope these notes may be useful to other beginners. I'll give also some examples in Python, to show that Haskell in fact is not so scary for beginners.
1. Lambdas
This is why I learned about Haskell. I was just curious what those lambdas are. A paper Conception, evolution, and application of functional programming languages by Paul Hudak was really helpful to get started (It's kind of old, and, probably, there are better introductions, but I read this one first).
Lambda expression is an essence of ‘function’: it's an expression of form
The value of this expression is a function, which takes one argument (x) and calculates something with it (an expression on the right hand side of the dot). There is much mathematical theory about lambdas, but sometimes I just think about 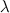 as a keyword to define functions. In fact, I was already used to lambdas in Python, where they look like:
as a keyword to define functions. In fact, I was already used to lambdas in Python, where they look like:
lambda x: expression with x
They were very useful in filter() and reduce(). They may be used almost anywhere where a function name is required, but lambdas don't have names. Hence, they are called Anonymous functions.
Sometimes in Python I give them names to define new functions on-the-fly
add_42 = lambda x: x + 42
Name add_42 now refers to a function. This is almost the same as defining functions in a more usual way:
def add_42(x):
return x+42
Now, what about Haskell? It's pretty much the same. \ symbol stays for 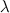 ,
, -> stays for dot:
\x -> expression with x
We can even give them names to define reusable functions:
add_42 = \x -> x + 42
Very similar, isn't it?
There is a subtle point. As soon as I started reading about Haskell, I saw lambda-expressions which looked a little bit strange at first:
\x -> \y -> an expression with x and y
What are those multiple ‘arrows’ I asked? The answer was really simple and very helpful to understand Haskell code.
All Haskell functions are functions of one argument. This may sound like a restriction initially, but then it turns out to be a very convenient concept. A function of n arguments may be represented as a function of one argument producing another function of n–1 arguments. This is called currying.
Once we know this, we can read any expression with many arrows:
\x -> (\y -> an expression with x and y)
The value of the expression is a function which takes an argument and produces another function which takes yet another argument. This expression as a whole behaves as if it were a function of two arguments. For example, we may apply such a function to two arguments in ghci (Haskell interpreter):
ghci> (\x -> \y -> x + y ) 3 4 7Of course, there is a shorthand form where we can write it as a function of two arguments (please note also that we don't need parentheses for function arguments):
ghci> (\x y -> x + y) 3 4 7
But it is very useful to know that internally every function of two or more arguments is actually a function of only one argument. This also helps reading function types later. For example, a type of map function reads like
map :: (a -> b) -> [a] -> [b]
I usually read it like this: ‘function map takes two arguments, a function from a to b and a list of a and produces a list of b’. But sometimes it is more natural to read as written:
map :: (a -> b) -> ([a] -> [b])
‘A function which takes a function from a to b and produces a function which converts a list of a to a list of b’.
These simple ideas about lambda functions were enough to get me started with Haskell and to understand most of the examples and tutorials.
2. Equals sign
As for me, equals sign = was probably the most important Haskell symbol to understand the language. I think its semantics is underemphasized in tutorials. For example, it's the only ‘keyword’ which is missing on a Haskell keywords' wikipage.
Unlike in most imperative languages where = means an assignemt (i.e. an action), in Haskell it means that its left hand side equals its right hand side.
‘Equals’ is not ‘becomes’. It means that something is equal to something else. Always. Just like in mathematics. a = b in Haskell means that a equals b by definition, a is equivalent to b.
So, = in Haskell serves to write definitions. It defines all sorts of things, but it defines them statically. It doesn't depend on the order of execution. It is something we may rely upon.
This may sound too evident, but this is a major difference for anyone with an imperative background. Now we may give names to our anonymous functions:
add = \x -> \y -> x + yTo tell the truth, it's not very readable, so most of the time functions are defined like this:
add x y = x + yBut this one is still a definition of
add.
3. Type classes
- define only an abstract interface (don't provide a default implementation)
- allow independent implementations (that is any class may become an instance of the type class if it implements class methods)
- are polymorphic by their nature and support inheritance
- don't have state variables
4. Monads
Now matter how gentle your introduction to Haskell is, sooner or later you stumble into the wall of Monads. Yes, there is some serious abstract mathematics behind them.
But I learned that it is not necessary to understand abstract mathematics to use monads, and they are indeed a very nice programming technique. They looked a little bit strange to me initially, but understanding monads is easier than memorizing countless OO design-patterns and using them right.
There are plenty of tutorials on monads, so I wont repeat them and expect that you've already read one or two. So, what's wrong with monads? For my imperatively prepared mind spoiled with years of object oriented thinking, monads looked strange. They may look like an abstract container class with a mystic >>= method:
class Monad m where return :: a -> m a (>>=) :: m a -> (a -> m b) -> m b fail :: String -> m aWell, if
return is a constructor, then why such a strange name? If this is a container class, how can I take values out? And what's the point of applying a function inside monad (>>= method, also known as bind) if we cannot take the result out of it?
Let's answer the last question first. What is the purpose of bind (>>=)? Monads are and are not containers. They are wrappers around computations rather than values (return). But they wrap computations not to store them conveniently in monadic boxes, but to link them together. Think standard bricks rather than boxes, or Adapter pattern. Each monad defines a standard interface to pass the result from one computation to the other (>>=). No matter what happens, the result is still in the same monad (even fail).
The most simple programming analogy I found is pipes in unix shell. Monads provide a unidirectional pipeline for computations. The same unix pipes do. For example:
$ seq 1 5 | awk '{print $1 " " $1*$1*$1 ;}'
1 1
2 8
3 27
4 64
5 125
seq produced a list of integers. awk calculated cubes for all of them. What's cool about this? We have two loosely coupled programs which work together. Text stream flows from left to write, each subsequent program in a pipe is capable to read this stream, do something with it, and output another text stream. Text stream is a common computation result, | binds computations together.
Monads are similar. >>= takes the inner computation from the monad on the left and puts it into the computation on the right, which always produces the same monad. You probably already know that lists and Maybe type in Haskell are monads. For example, if we have a simple computation which returns a pair of a number and its cube into the monad:
\x -> return (x, x^3)
then we can ‘pipe’ the list into this computation:
ghci> [1,2,3,4,5] >>= \x -> return (x,x^3) [(1,1),(2,8),(3,27),(4,64),(5,125)]
Please note that we received a list of pairs. It's the same monad (the list). But if we ‘pipe’ a Maybe value into the same computation, we get the same monad as input (Maybe):
ghci> Just 5 >>= \x -> return (x,x^3) Just (5,125)
You see, we can construct a pipeline of two computations, and the behaviour of this pipeline depends on the context (i.e. on the Monad instance), not on the computations themselves. Unlike unix pipes, Monads are type-safe, type system takes care that the output of one monadic computation is compatible with the input of the other. And unlike unix pipes, we can define our own binding rules (>>=). Like ‘don't join more than 42 computations in a row’ or ‘look at the input, and do one thing or the other’. Monads encapsulate rules how to bind computations together.
Now, I hope, you understand monads at least as well as I do (not necessarily perfectly). I'd like to discuss some mnemonics. Why return is named ‘return’?
In most languages, return returns result from a function. In Haskell, it acts as constructor for monads. Weird. Well, let's look at how >>= works, we see that it extracts a value from the monad on the left, and then binds it to the argument of the function on the right. This function should return the result back into monad, so that the next >>= can work. This is the first mnemonics.
The second mnemonics. On the top level any Haskell program is executed in IO monad (main's type is IO ()), which can do input/output (and sequential operations in general). Thus, monadic code is executed on the top level and it calls any pure code when necessary, not otherwise. So any pure value if not discarded is eventually returned into the monad of the caller.
With these two explanations the name return does not sound so weird for me as before. I don't pretend these explanations are technically correct.
The next question, how to take a value of the computation out of the monad? Well, it's not always possible by design. For example, you cannot take a pure value outside of the IO monad. If we have such a one-way monad, the only thing we can do, is pipeline the value to the next computation. Fortunately, Haskell has a nice do-notation, which makes such pipelining look almost identical to imperative programming languages. These two programs describe the same thing, with do-notation:
main :: IO ()
main = do
name <- getLine
putStrLn ("Hi, " ++ name)
and with explicit >>=:
main :: IO ()
main = getLine >>= \name -> putStrLn ("Hi, " ++ name)
An equivalent Python program:
from sys import stdin, stdout
if __name__ == "__main__":
name = stdin.readline()
stdout.write("Hi, " + name)
However, sometimes it is possible to take the pure value out of the monadic computation. This is not possible with the standard monad interface, so the developer of the monad should provide means to extract values. For example, it is possible to extract values from Maybe monad using fromMaybe function:
ghci> fromMaybe 0 $ Just 3 3 ghci> fromMaybe 0 $ Nothing 0
Résumé on monads
So, bind (>>=) allows to put various monadic computations together and combine them. Anywhere, where we have a chain of computation, monads fit naturally. Particular monad implementation may encapsulate custom rules of combining two computations together. Name return may be confusing for beginners, but we have to remember that it returns a value into the monad, not from the monad. Understanding this helped me a lot.